Gridex Protocol

November 2022

 

Abstract

The Gridex Protocol is a permissionless and non-custodial trading protocol consisting of a set of persistent, non-upgradable smart contracts on the Ethereum blockchain. Unlike the current mainstream decentralized exchanges based on the Automated Market Maker (AMM) model, Gridex is based on order books. With our novel Grid Maker Order Book (GMOB) model, we have significantly reduced the resource consumption of running an order book based system, allowing us to deploy and run it on the Ethereum mainnet while making the gas cost comparable to that of AMMs.

1. Introduction

Since 2020, the surge of decentralized exchanges (DEXs) based on the Automated Market Maker (AMM) model – or more precisely, the Constant Function Market Maker (CFMM) exemplified by Uniswap; has led to the AMM model becoming the norm of DEXs. The minimal resource consumption of the AMM model compared to the central limit order book (CLOB) model - mainly utilized in traditional exchanges, makes it the key to easily implementing an on-chain system of smart contracts. DeFi would not be where it is without AMM, but it cannot meet the diverse needs of traders and market makers due to impermanent loss, high slippage, and lack of flexibility. Particularly in the AMM model, the greater the market volatility, the greater the risk of impermanent loss faced by liquidity providers (LPs). Consequently, the AMM model is most suitable for less volatile trading pairs, such as swaps between stablecoins.

The algorithms of matching engines, commonly implemented in centralized exchanges (CEXs) based on the CLOB model, consume a large number of resources making it difficult to deploy and run on the Ethereum blockchain. Some DEXs have attempted to solve this issue by implementing matching engines and order books off-chain. However, such solutions not only increase the risk of centralization (to a certain extent) but also limit their ability to interact with other protocols, making it impossible to utilize or contribute to the open ecosystem of Ethereum effectively. Henceforth, we have created the Grid Maker Order Book (GMOB) model and the Grid Price Linear Movement (GPLM) algorithm, which we describe in Sections 2 and 3, respectively. Compared with the algorithm of matching engines, GPLM is simplistic: resource consumption is significantly reduced, and it is easily implemented in smart contracts on the Ethereum blockchain.

2. Grid Maker Order Book

The Gridex Protocol is based on the GMOB model. In the GMOB model, maker orders are similar to limit orders in the CLOB model. However, there are three distinct differences:

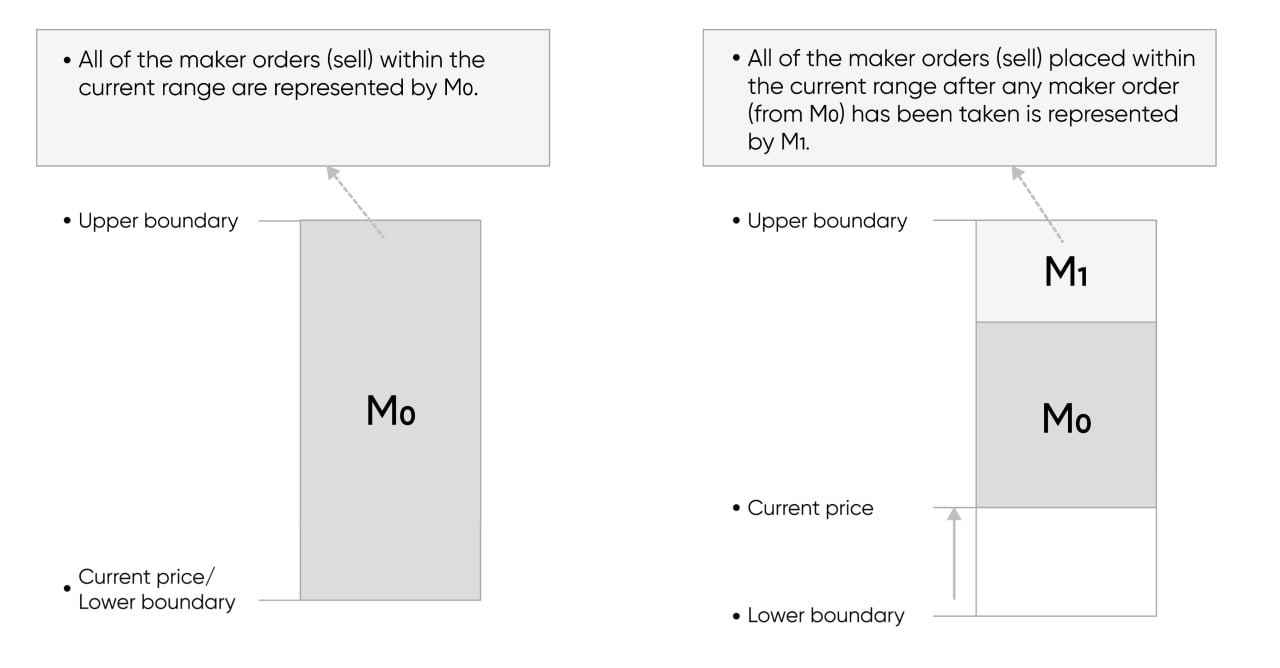
1. Maker orders are bounded within a very narrow price range (percentage based) instead of a specific price. The percentage of a range is called the 'resolution' (Section 4). The upper and lower boundaries of every range are called the 'boundaries'. Boundaries are similar to the ticks in Uniswap V3 but have different usage.
2. Unlike limit orders, maker orders are never executed immediately and are added to the order book in the GMOB model. As maker orders add liquidity to the order book, the Gridex Protocol awards maker orders with negative trading fees. Therefore, traders will be granted a maker fee when a maker order is executed (Section 4).
3. A significant difference on the operational level between maker orders and limit orders is that once the maker orders are filled, the user must manually execute the 'Collect' operation to get back the filled assets and the rewarded fees.

3. GPLM Algorithm

In this section, we explain how a taker order (swap) functions.

We define the following terms as:

Table 1

Terminology	Notes
$token0$	-
$token1$	-
$zeroForOne$	A taker uses $token0$ to exchange for $token1$
$oneForZero$	A taker uses $token1$ to exchange for $token0$
$P$	The price of $token0$ in terms of $token1$
$P_n$	The new price after a taker order has been filled
$P_c$	Current price
$P_a$	The average transaction price of a taker order
$P_b$	When the trading direction is $zeroForOne$, $P_b$ is the lower boundary of the range When the trading direction is $oneForZero$, $P_b$ is the upper boundary of the range
$M$	When the trading direction is $zeroForOne$, $M$ is the amount of $token1$ from all maker orders in the current range When the trading direction is $oneForZero$, $M$ is the amount of $token0$ from all maker orders in the current range
$T_o$	The amount of tokens received by the taker (outputted)
$T_i$	The amount of tokens submitted by the taker (inputted)
$exactInput$	Output calculated based on input by the taker
$exactOutput$	Input calculated based on output by the taker

When $T_o$ is less than or equal to $M$, we use the following equation to calculate the price after the transaction:

Equation 3.1

$$\begin{aligned} P_n=P_c+\frac{T_o(P_b-P_c)}{M} \end{aligned}$$

 

We use the following equation to calculate the average transaction price for the taker:

Equation 3.2

$$\begin{aligned} P_a=\frac{P_n+P_c}{2} \end{aligned}$$

 

When the taker uses the $exactOutput$ operation, the following equations are used to calculate $T_i$:

Equation 3.3 ($zeroForOne$)

$$\begin{aligned} T_i=\frac{T_o}{P_a} \end{aligned}$$

 

Equation 3.4 ($oneForZero$)

$$\begin{aligned} T_i={T_oP_a} \end{aligned}$$

 

When $P_n$ is specified by the taker, Equation 3.1 is used to calculate $T_o$:

 

$$\begin{aligned} T_o=\frac{M(P_n-P_c)}{P_b-P_c} \end{aligned}$$

 

When the taker uses $exactInput$, and the direction of the trade is $zeroForOne$, by using Equations 3.1, 3.2, and 3.3, we have:

Equation 3.5

$$\begin{aligned} T_o=\frac{2MT_iP_c}{2M-T_i(P_b-P_c)} \end{aligned}$$

 

When the taker uses $exactInput$, and the direction of the trade is $oneForZero$, Equations 3.1, 3.2, and 3.4 result in:

 

$$\begin{aligned} T_o=\frac{M\sqrt{P_c^2+\frac{2T_i(P_b-P_c)}{M}}-MP_c}{P_b-P_c} \end{aligned}$$

 

The square rooting operation consumes a large amount of resources on-chain. To save gas cost, we calculate $T_o$ in the $oneForZero$ case by redefining $P\rightarrow\frac{1}{P}$ in Equation 3.5. We obtain:

 

$$\begin{aligned} T_{o}=\frac{\frac{2 M T_{i}}{P_{c}}}{2 M-T_{i}\left(\frac{1}{P_{b}}-\frac{1}{P_{c}}\right)} \end{aligned}$$

 

'Linear' in the Grid Price Linear Movement (GPLM) algorithm is representative of the fact that within a price range, the price change caused by a taker order is linearly proportional to the quantity of tokens taken away.

A typical case of how the GPLM algorithm functions is illustrated in the figure below.

As shown in the figure, when a user exchanges $token1$ for $token0$ ($oneForZero$), the price of $token0$ will rise after the exchange.

In the following steps, maker and taker orders are sell and buy, respectively.

1. We assume that the current price ($P_c$) falls exactly on the lower boundary of the price range. We express the liquidity of all the maker orders in this price range as $M_0$.
2. A taker order is placed where the buy amount ($T_o$) is less than the total amount of maker orders in the current range ($M$). The price after the transaction is given by Equation 3.1. The amount of each maker order in $M_0$ will be filled by $\frac{T_o}{M}$ ($M$ given by Table 1). The average filled price of the taker order can be formulated by using Equation 3.1 in conjunction with Equation 3.2. If the buy amount ($T_o$) exceeds $M$, proceed directly to step 4.
3. After $M_0$ is first traded by a taker, if there are still users who place maker orders in this range, these new orders are expressed as $M_1$. When all maker orders of $M_0$ are filled by takers, a check is performed to see whether $M_1$ exists. If so, $M_1$ is replaced by $M_0$, and steps 2 and 3 are repeated until there are no more maker orders in the current range; then, the algorithm proceeds to step 4. If not, directly proceed to step 4.
4. When all maker orders in the range are executed, and the taker order which bought out the last maker orders is not entirely filled, the price will touch the upper boundary of the range and enter the next range. Then, repeat from step 1 to calculate the future price movement.

4. Grids and Fee Levels

The Gridex Protocol will initially support 3 types of grids:

Grid Resolution ($G\%$)	Maker Fee	Taker Fee
0.01%	-0.008%	0.01%
0.05%	-0.04%	0.05%
0.3%	-0.24%	0.3%

A grid resolution ($G\%$) defines the step size ($100G$) used to create boundary values $P_b(i)$, which are indexed by integer values $i$. These can be determined by the following functions:

 

$$\begin{aligned} P_b(i)=1.0001^{(100G)i} \end{aligned}$$

 

Similarly, $i$ can be derived from a given $P_b$ and $G\%$:

 

$$\begin{aligned} i=\frac{1}{100G}log_{1.0001}(P_b) \end{aligned}$$

 

5. GDX Token

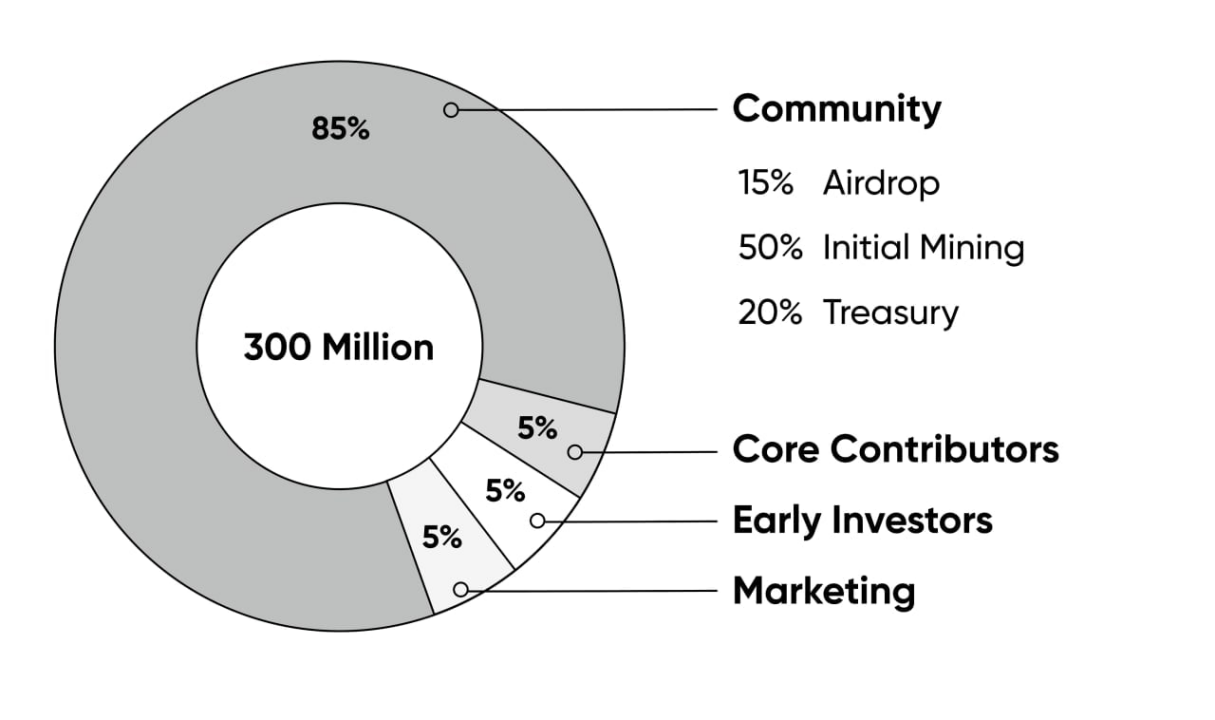
GDX is the native governance token of the Gridex Protocol. It has a maximum supply of 300 million, which will be fully issued before the official launch of Gridex. 100% of the protocol fees will be used to buyback and burn GDX.

Initial Allocation

85% of GDX to the Gridex community, which will include:

1. Airdrop: 15% ‘45 million GDX’, airdropped to DeFi users before the official launch of Gridex.
2. Initial Mining: 50% ‘150 million GDX’, rewarded to trading users of Gridex within one month after the official launch.
3. Treasury: 20% ‘60 million GDX’, reserved to fund the continued development of the Gridex Protocol, with 4-year vesting.

15% of GDX to core contributors, early investors, and marketing, which will be equally split between all three entities.

6. Roadmap

November 2022

• Official Website Launch
• Whitepaper Launch
• Airdrop Launch

December 2022

• Smart Contract Audit
• Gridex Protocol Open Source
• Gridex Protocol Testnet Launch
• Airdrop End

January 2023

• Airdrop Distribution
• Gridex Protocol Official Launch
• Initial Mining Launch

February 2023

• Initial Mining End
• Buyback and Burn GDX Begin

March 2023

• On-chain Governance System Launch